4.基于概率论的分类方法：朴素贝叶斯
2017-12-29 16:11:28 42 举报AI智能生成
概率图模型
作者其他创作
大纲/内容
条件概率
条件概率
贝叶斯准则
使用贝叶斯准则来分类
类条件概率
分类决策
如果p(c1|x,y) > p(c2|x,y)，则属于类别c1
如果p(c1|x,y) < p(c2|x,y)，则属于类别c2
极大似然估计
EM算法
贝叶斯决策理论
优点
在数据较少的情况下仍然有效
可以处理多类别问题
缺点
对于输入数据的准备方式较为敏感
贝叶斯决策理论
假设一个数据集由两类数据组成
假设找到了两类数据的统计参数
p1(x,y)表示数据点(x,y)属于类别1的概率
p2(x,y)表示数据点(x,y)属于类别2的概率
如果p1(x,y) > p2(x,y)，则类别为1
如果p1(x,y) < p2(x,y)，则类别为2
贝叶斯分类器
贝叶斯分类器一般过程
搜集数据
数据预处理
数值型
布尔型
训练分类器
计算不同的独立特征的条件概率
测试分类器
条件风险
应用
e.g.文本分类
常见贝叶斯分类器
朴素贝叶斯分类器
定义
设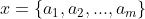
为一个待分类项，而每个a为x的一个特征属性
有类别集合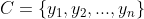
计算,P(y_2|x),...,P(y_n|x))
如果=max\{P(y_1|x),P(y_2|x),...,P(y_n|x)\})
，则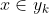
采用属性条件独立性假设 
计算各类条件概率
给定已知类别训练样本集合
统计得到在各类别下各个特征属性的条件概率估计 ,P(a_2|y_1),...,P(a_m|y_1);P(a_1|y_2),P(a_2|y_2),...,P(a_m|y_2);...;P(a_1|y_n),P(a_2|y_n),...,P(a_m|y_n))
根据贝叶斯准则有： =\frac{P(x|y_i)P(y_i)}{P(x)})
分母对于所有类别为常数，只要最大化分子
朴素贝叶斯假定属性相互独立 P(y_i)=P(a_1|y_i)P(a_2|y_i)...P(a_m|y_i)P(y_i)=P(y_i)\prod^m_{j=1}P(a_j|y_i))
流程如下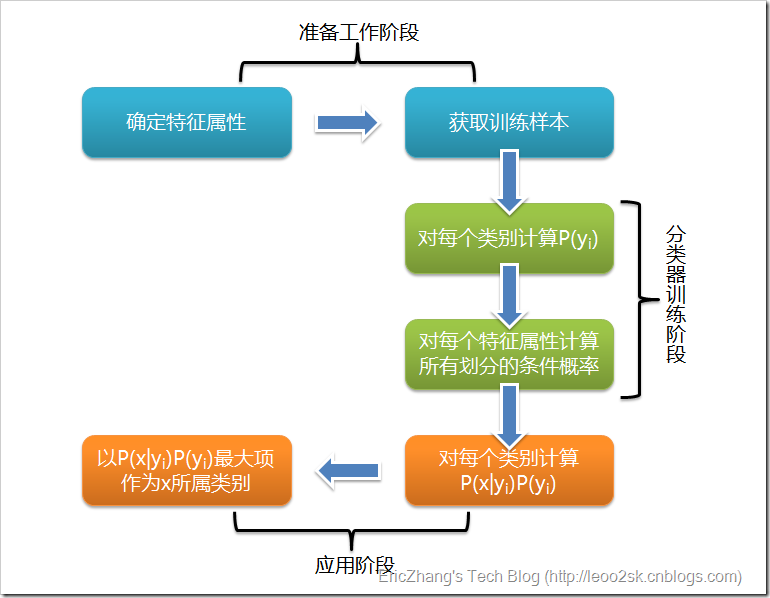 
半朴素贝叶斯分类器 
条件互信息
独依赖分类器
SPODE分类器
假定所有属性都依赖于同一个属性，即超父属性
一般通过交叉验证等模型选择方法来确定超父属性
TAN分类器
基础：最大带权生成树算法
步骤
先求每个属性之间的互信息来作为他们之间的权值
找一个根变量，然后依次将图变为有向图
添加类别y到每个属性的的有向边
贝叶斯网
借助有向无环图来刻画属性之间的依赖关系，并用条件概率表来描述属性的联合概率分布
构成B(G，Q)
G：贝叶斯网的结构，由一个有向无环图表示
结点：每个结点代表一个属性
边：若两个属性有直接依赖关系，则由一条边连接
三个变量之间的典型依赖关系
同父结构
V型结构
顺序结构
Q：参数，定量描述属性依赖关系
学习：评分搜索
最小描述长度准则
0 条评论
下一页
