EM算法笔记
2016-12-01 21:34:11 0 举报AI智能生成
EM算法是一种迭代优化技术，主要用于含有隐变量的概率模型参数估计。它通过两步交替进行：E步（Expectation）计算期望，M步（Maximization）最大化期望。在E步，算法计算在当前参数下隐变量的后验概率；在M步，算法更新参数以最大化这个后验概率的期望。这个过程不断重复，直到收敛。EM算法是处理缺失数据、混合模型等复杂问题的有效工具，但也可能陷入局部最优。
作者其他创作
大纲/内容
极大似然估计的一般步骤
写出似然函数
对似然函数取对数，并整理
求导数，令导数为0，得到似然方程
解似然方程，得到的参数即为所求
EM的算法流程：
流程
输入：观测数据 Y，不可观测数据 Z
输出：参数
step1：给出参数初始化值 θ0
step2：E步
记 θn为第n 次迭代后参数的估计值
在第 n+1次迭代的E步，求期望（ Q 函数）
step3：M步
求 Q函数的极大值点，来作为第 n+1次迭代所得到的参数估计值 θn+1
θn+1=argmaxθQ(θ|θn)
迭代E和M步，直到满足停止条件
EM算法的核心在于E步中Q函数的求解
EM算法的收敛性
定理1
观测数据的似然函数
P(Y|θ)
通过EM算法得到的序列 单调递增：
定理2
(1) 如果 有上界，则 收敛到某一值L ∗
(2) 在 函数与 满足一定条件下，由EM算法得到的参数估计序列的收敛值 是 的稳定点
EM算法的引入
EM算法是含有隐变量的概率模型参数的极大似然估计方法或极大后验概率估计法
EM算法是一种迭代方法
Jensen不等式
凸函数
设f是定义域为实数的函数，如果对于所有的实数x满足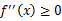 
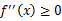
则f是凸函数
当x是向量时，如果其hessian矩阵H是半正定的，即满足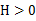 
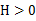
则f是凸函数
Jensen不等式
如果f是凸函数，X是随机变量
特别地，如果f是严格凸函数：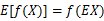 
成立当且仅当：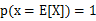 
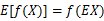成立当且仅当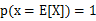： EM算法
给定的训练样本是clip_image023，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大
p(x,z)的最大似然估计如下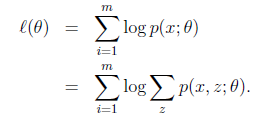 
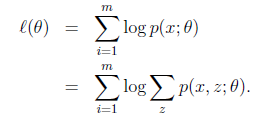
思路
不能直接最大似然函数
E步
可以不断地建立似然函数的下界
基于Jensen不等式
似然函数
l(θ)=∏j=1NP(yj|θ)=∏j=1N∑zP(z|θ)P(yj|z,θ)
记对数似然函数为
L(θ)=lnP(Y|θ)=ln∑zP(z|θ)P(Y|z,θ)
L(θ)−L(θn)=ln(∑zP(z|θ)P(Y|z,θ))−lnP(Y|θn)
则使用Jensen不等式有：
定义一个函数
l(θ|θn)≜L(θn)+∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(Y|θn)P(z|Y,θn)
L(θ)≥l(θ|θn)
第 次迭代结束后， 的一个下界为 。另外，有等式 成立
结论
的下界为
从而，任何能让 增大的 ，也可以让 增大
能满足 l(θn+1|θn)>l(θn|θn) 的 θn+1 ，一定更能满足L(θn+1)>l(θn|θn)
EM算法通过优化对数似然在当前的下界，来间接优化对数似然
M步
然后优化下界
θn+1=argmaxθl(θ|θn)
把 中的几个与 无关的量去掉，得到：
0 条评论
下一页
